Unit 4: Building a Logical Data Model
Unit 4: Building a Logical Data Model

In this unit, you’ll apply the concepts learned so far to evaluate a statistical table and the Conceptual Data Model and extend the model to create a Logical Data Model with fully defined variables and value sets.
Logical Data Model Table
Further developing the Conceptual Data Model to create the Logical Data Model involves adding more detail to the statistical measure and every variable. The benefit of using a table for the modelling exercise is that the variable types and value sets are relatively easy to identify.
For each variable, review the definitions for variable types and identify if the variable is categorical or numeric and its subtype (nominal or ordinal for categorical and discrete or continuous for numeric). Once the variable type has been identified, identify the value sets.
The observation unit has been introduced to this table to represent the values being published in the table for the primary measure. The variable type is numeric, and the number format is determined by the way the numbers are presented in the table.
Select the table to enlarge. ![]()
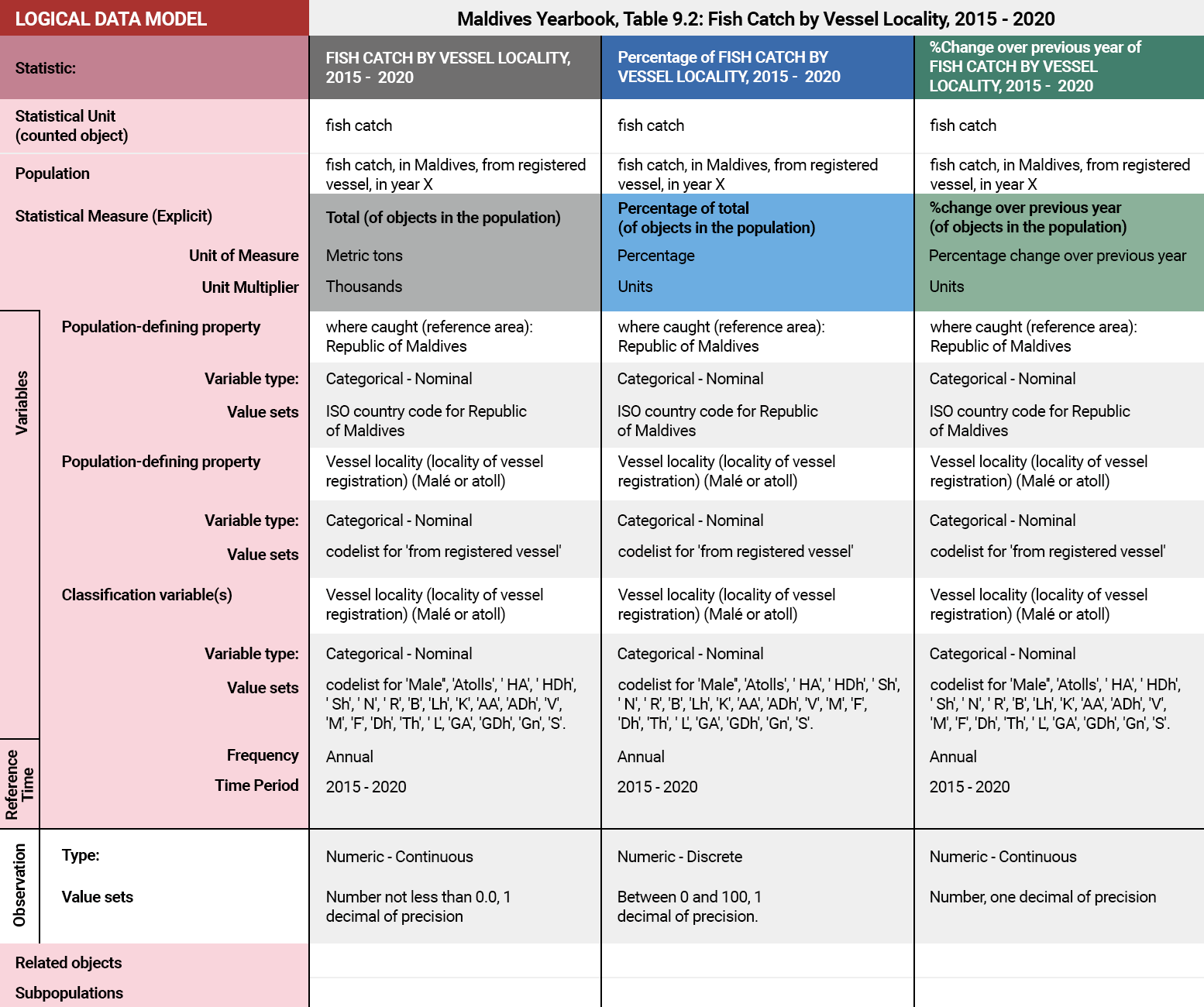

Variable types are either categorical or numeric:
- A categorical variable (also called qualitative variable) refers to a characteristic that can’t be quantified.
- A numeric variable (also called quantitative variable) is a quantifiable characteristic whose values are numbers.
Categorical variables can be either nominal or ordinal.
- Nominal: A nominal variable is one that describes a name, label or category without natural order. Sex and type of dwelling are examples of nominal variables. Example: Variable = “Sex”, Value set = “male”, “female”.
- Ordinal: An ordinal variable is a variable whose values are defined by an order relation between the different categories. “Behaviour” is ordinal because the category “Excellent” is better than the category “Very good,” which is better than the category “Good,” etc. There is some natural ordering. Example: Variable = “Behaviour”, Value set = “Excellent”, “Very Good”, “Good”, “Bad”, “Very Bad”.
Numeric variables may be either continuous or discrete.
- Discrete: A discrete variable can only assume a finite number of real values within a given interval. An example of a discrete variable would be the score given by a judge to a gymnast in competition: the range is 0 to 10 and the score is always given to one decimal (e.g. a score of 8.5). You can enumerate all possible values (0, 0.1, 0.2…) and see that the number of possible values is finite: it is 101. Example: Variable = “Score”, Value set = A real number greater than or equal to 0 and less than or equal to 10 with one decimal point of precision.
- Continuous: A variable is said to be continuous if it can assume an infinite number of real values within a given interval. For instance, consider the height of a student. The height can’t take any values. It can’t be negative, and it can’t be higher than three metres. But between 0 and 3, the number of possible values is theoretically infinite. A student may be 1.6321748755 … metres tall. Example: Variable = “Height of student”, Value set = A real number greater than or equal to 0 and less than or equal to 3.
Logical Data Model – Codelists
The representation of statistics in the Conceptual and Logical Data Models provides a good working tool to analyse a table, or group of tables, and determine how it (they) should be modelled. The models are also a good source of documentation of the statistics relevant to the organisation.
This representation however also has its limitations in terms of representing categorical variables with codelists. It’s therefore recommended that once this initial analytical exercise has been completed and a satisfactory set of definitions established, the categorical variables have the codelists for their valuesets elaborated in a set of codelist tables for ease of reference and ease of use.
Select the table to enlarge. ![]()
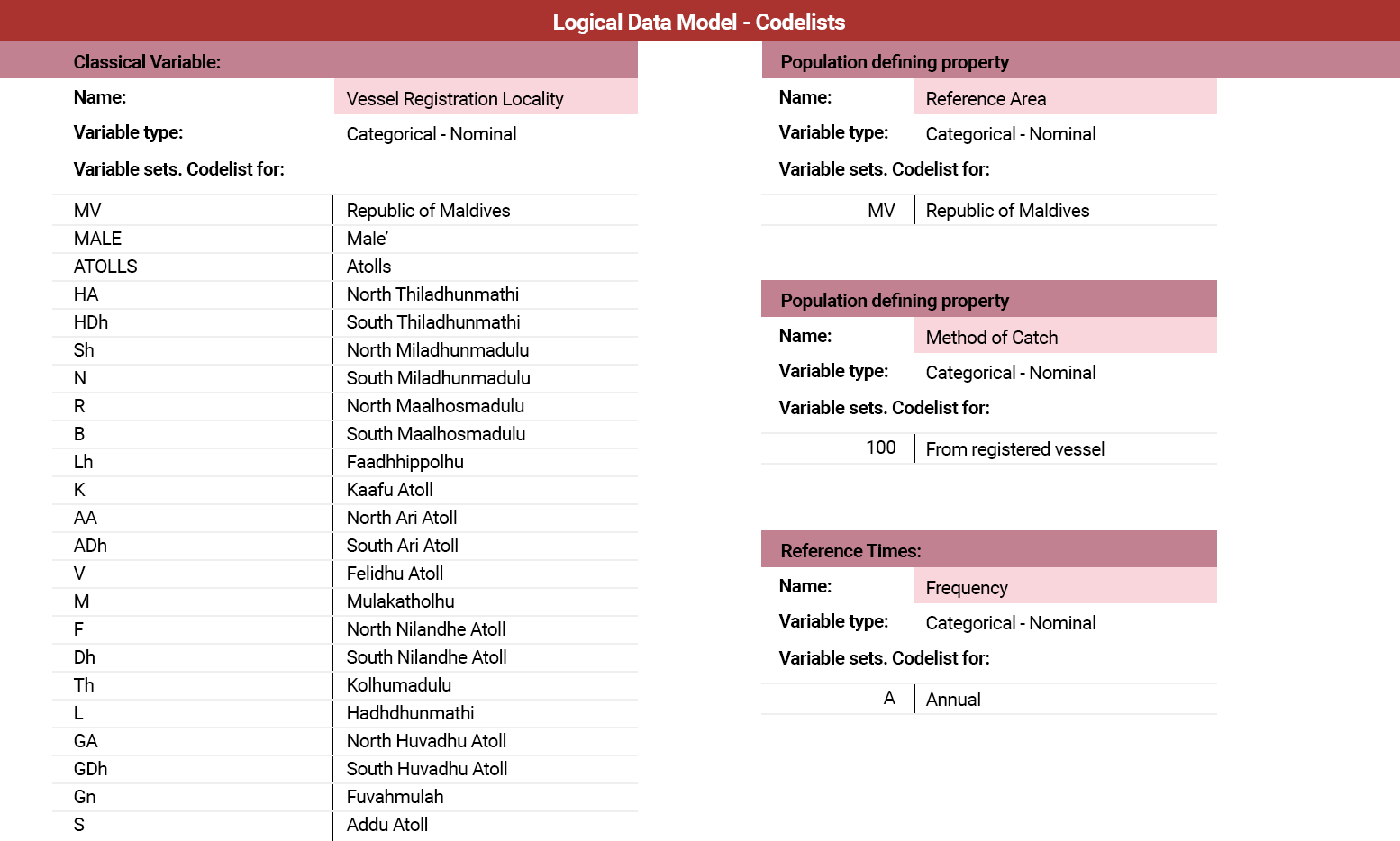

What do you know?
You have now completed this Introduction to Structural Modelling for Statisticians, but before moving on to the module summary, try this final question.
Further developing a Conceptual Data Model to create the Logical Data Model involves adding more detail to the statistical measure and every variable. For each variable, you need to identify if it’s categorical or numeric and its subtype (nominal or ordinal for categorical and discrete or continuous for numeric).
Which of the following correctly describe the four subtypes?
Select all that apply and then select Submit.
Categorical variables can be either nominal or ordinal.
- A nominal variable is one that describes a name, label or category without natural order.
- An ordinal variable is a variable whose values are defined by an order relation between the different categories.
Numeric variables may be either discrete or continuous.
- A discrete variable can only assume a finite number of real values within a given interval.
- A variable is said to be continuous if it can assume an infinite number of real values within a given interval.
Categorical variables can be either nominal or ordinal.
- A nominal variable is one that describes a name, label or category without natural order.
- An ordinal variable is a variable whose values are defined by an order relation between the different categories.
Numeric variables may be either discrete or continuous.
- A discrete variable can only assume a finite number of real values within a given interval.
- A variable is said to be continuous if it can assume an infinite number of real values within a given interval.
Categorical variables can be either nominal or ordinal.
- A nominal variable is one that describes a name, label or category without natural order.
- An ordinal variable is a variable whose values are defined by an order relation between the different categories.
Numeric variables may be either discrete or continuous.
- A discrete variable can only assume a finite number of real values within a given interval.
- A variable is said to be continuous if it can assume an infinite number of real values within a given interval.